Our research group is mainly concerned with exploring open problems in combinatorics, discrete mathematics and graph theory.
Research areas
Graph Theory
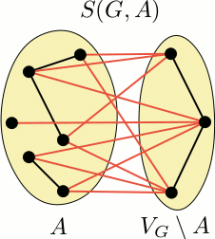
Over the past decades, graph theory has found many applications in various areas of human activity from network designing (electrical, water, social), allocation of mobile or broadcasting frequencies to various types of optimization (in traffic, searching, etc.). Our group focuses mainly on the study of a special class of graphs derived from partially ordered sets, so-called cover-incomparability graphs, their properties and the complexity of their recognition. Another area that is currently at the center of our interest is the study of equivalences on graphs defined by various graph operations, such as Seidel's switching.
Graph theory in Chemistry
In this area, we primarily focus on the study of so-called Wiener Index of molecular graphs. Harry Wiener introduced this index to determine the approximation formula of the boiling point of paraffin.
Since then, the Wiener Index has become one of the most commonly used molecular descriptors and it is currently used e.g. for pre-screening of drug molecules.
We are mainly interested in determining the extremal values of Wiener index for important graph classes.
Computational complexity
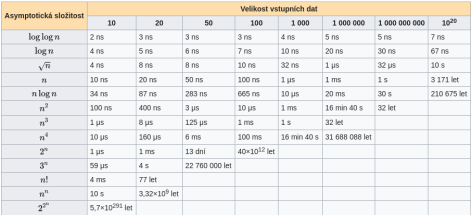
Asymptotic complexity is one of the essential tools to compare algorithm efficiency and speed. The particular problem is the determination of its time complexity with respect to the size of the input, which can be enormous for relatively simple tasks and relatively small inputs (e.g. hundreds of years). Finding the boundary for polynomial complexity for different tasks on graphs is at the center of our interest (see known problem P versus NP).
Groups of reflections and their applications
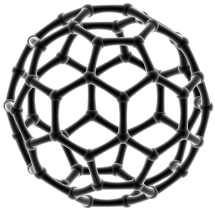
Group of reflections describe (among other things) natural symmetries of regular and semiregular n-dimensional object, e.g. Platonic solids. We study propertis of special functions related to reflection groups orbit functions. Corresponding symmetries are used in the study of generalized discrete fourier transforms.
 Presentation card
Presentation card
Contact persons:
Y RNDr. Jana Maxová, Ph.D. - team representative
b jana.maxova@vscht.cz
e 22044 5039
Y Ing. Lenka Háková, Ph.D.
b lenka.hakova@vscht.cz
e 22044 5035
Y Ing. Tomáš Hejda, Ph.D.
b tomas.hejda@vscht.cz
e 22044 4349
Y RNDr. Eva Jelínková, Ph.D
b eva.jelinkova@vscht.cz
e 22044 5030
Y Doc. RNDr. Daniel Turzík, CSc.
b daniel.turzik@vscht.cz
e 22044 5036
Recent papers
- Bok, Jan & Maxová, Jana. (2018). Characterizing Subclasses of Cover-Incomparability Graphs by Forbidden Subposets. Order. 10.1007/s11083-018-9470-7.
- Jelínek, V.; Jelínková, E.; Kratochvíl, J. On the hardness of switching to a small number of edges. Lecture Notes in Computer Science, Springer, 2016.
- Háková L.; Tereszkiewicz A. On Generalization of Special Functions Related to Weyl Groups. Acta Polytechnica, Journal of Advanced Engineering 2016, 56 (6), 440–447
- Háková L.; Hrivnák J.; Motlochová L. On cubature rules associated to weyl group orbit functions. Acta Polytechnica, Journal of Advanced Engineering 2016, 56 (3), 202–213
- Hejda, T.; Pelantová, E. Spectral properties of cubic complex Pisot units Mathematics of Computatio. 2016.
- Maxová, J.; Dubcová, M.; Pavlíková, P.; Turzík, D. Which k-trees are cover-incomparability graphs? Discrete Applied Mathematics, 2014.
- Jelínková, E.; Kratochvíl, J. On Switching to H-Free Graphs. Journal of Graph Theory, 2014.
- L.Háková, A. Tereszkiewicz, On immanant functions related to Weyl groups of A_n, J. Math. Phys., Vol.55, Issue 11, 2014
- Maxová, J.; Turzík, D. Which distance-hereditary graphs are cover-incomparability graphs? Discrete Applied Mathematics, 2013.