Research involving dynamical systems has a long tradition in our department. The first seminar devoted to the systems of differential equations and general theory of dynamical systems was established more than 30 years ago. We are currently investigating a large number of problems associated with dynamical systems, both at the theoretical and application levels.
Research areas
Qualitative theory of dynamical systems
Systems of ordinary differential equations are examined with respect to their geometrical and qualitative properties; they are studied within the framework of general qualitative theory of dynamical systems.
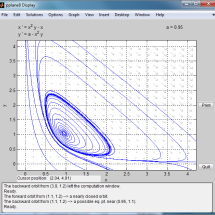
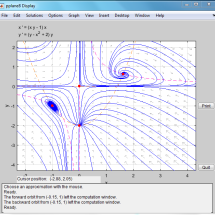
Discontinuity appears in many applications including chemical engineering, biology, control theory, etc. It can be an integral, natural feature of the system, or it can be caused for instance by external interference. Piecewise smooth dynamical systems possess a fascinating and complex dynamics. The techniques available for the continuous case enable us to investigate the phase portrait, stability, bifurcations and other local or global properties of discontinuous so-called Filippov systems.
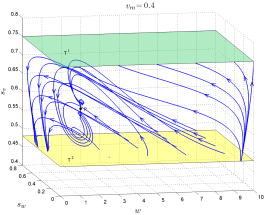
Dynamical system of spiders on the vineyard with the balloon effect.
M. Biák: Piecewise smooth dynamical systems. PhD Dissertation, UCT Prague, 2015
Reconstruction of the dynamics from time-series
The dynamics reconstruction is based on the time delay approach, relying on the Takens embedding theorem. The time-series data, i.e. the projection of the dynamical system to a real interval, describe the dynamical system only partially. The method is able to qualitatively reconstruct the behaviour of the whole dynamical system; it can be applied to the time-series data originated for instance from chemical or medical problems.
Solving differential equations
Concerning the numerical methods for ordinary and partial differential equations we are oriented on the method of finite elements and finite volumes, marginally also the method of finite differences. Regarding the analytical methods we focus primarily on the Laplace
transform, as an efficient tool to solve linear partial differential equations appearing in the technical practice.
Fluid mechanics and thermodynamics
In the field of computational fluid dynamics (CFD), we use software OpenFOAM to simulate multiphase flows, for example in separation columns. In theory, we study the mathematical analysis of equations describing the flows of compressible fluids, among others chemically reacting mixtures.

Chaos theory
The chaos theory deals with nonlinear dynamical systems, characterized by complex, bounded, undamped and nonperiodic behaviour, so called deterministic chaos. Although it is deterministic, the precise trajectories are unpredictable due to sensitive dependence on the initial conditions.
Thermodynamics of information
Information thermodynamics combines information theory with the concepts of classical thermodynamics. The theory meets applications in a lot of physical processes.
Optimization and control theory
In the control theory we investigate the models of biochemical processes and their properties such as controllability, observability and stability. Further we estimate the parameters of the model, or perform simulations. From the perspective of possible applications, we are interested in the problem of optimal control or possible dimension reductions of the models.
Mathematical finance
The parabolic partial differential equations describing the dynamics of financial markets are studied. We focus on numerical solution of special difusion equation following from the Black–Scholes model for financial derivatives pricing.
Numerical methods on Clifford algebras
Within a long-term cooperation with the University of Hamburg, we study the numerical linear algebra for quaternions, and other commutative or noncommutative algebras in R4. Quaternions play currently a key role in robotics and computational graphics development. Another non-commutative algebra in R4, so called coquaternions, finds its applications for instance in complex problems of quantum chemistry and physics.
Presentation card
Contact persons
Y Mgr. Šimon Axman, Ph.D. - team representative
b simon.axmann@vscht.cz
e 22044 5030
Y RNDr. Lenka Červená, Ph.D.
b lenka.cervena@vscht.cz
e 22044 5031
Y RNDr. Miroslava Dubcová, CSc.
b miroslava.dubcova@vscht.cz
e 22044 5031
Y Ing. Bohdan Hejna, Ph.D.
b bohdan.hejna@vscht.cz
e 22044 5037
Y Ing. Martin Isoz, Ph.D.
b martin.isoz@vscht.cz
e 22044 4349
Y Prof. RNDr. Drahoslava Janovská, CSc.
b drahoslava.janovska@vscht.cz
e 22044 5040
Y Prof. RNDr. Milan Kubíček, CSc.
b milan.kubicek@vscht.cz
e 22044 3095
Y Mgr. Jana Němcová, Ph.D.
b jana.nemcova@vscht.cz
e 22044 5038
Y RNDr. Pavel Pokorný, CSc.
b pavel.pokorny@vscht.cz
e 22044 5033
Y Doc. RNDr. Carmen Simerská, CSc.
b carmen.simerska@vscht.cz
e 22044 5040
Recent publications
- Janovska, Drahoslava; Opfer, Gerhard: The Relation Between the Companion Matrix and the Companion Polynomial in R-4 Algebras, ADVANCES IN APPLIED CLIFFORD ALGEBRAS, Volume: 28, Issue: 4, Article Number: UNSP 76, Published: SEP 2018
- Isoz M., Haidl J.: CFD analysis of gas flow through corrugated sheet structured packing: Effects of packing geometry. Industrial & Engineering Chemistry Research, 57(34), 11785–11796, 2018.
- van Schuppen J., Xi K., Němcová J.: A Subalgebraic Procedure for System Identification of a Continuous-Time Polynomial System. IFAC-PapersOnLine, 51, 395-400, 2018.
- Hejna B.: Information Transfer and Thermodynamic Point of View on Goedel Proof, in Ontology in Information Science, 280-300, 2018.
- Axmann Š., Mucha P.B., Pokorný M.: Steady solutions to the Navier-Stokes-Fourier system for dense compressible fluid. Topol. Methods Nonlinear Anal., 52, 2018.
- Hejna B.: Informační termodynamika IV. ; Goedelovy věty, přenos informace, termodynamika a Caratheodoryho věty, VŠCHT Praha, 2017.
- Kočí P., Isoz M. et.al. 3D reconstruction and pore-scale modeling of coated catalytic filters for automotive exhaust gas aftertreatment. Catalysis Today, 2017.
- Janovská D., Opfer G.: The number of zeros of unilateral polynomials over coquaternions and related algebras. Electronic Transaction on Numerical Analysis, 46, 55-70, 2017.
- Němcová J., van Schuppen J.: Checking Algebraic Reachability of Polynomial and Rational Systems, IFAC-PapersOnLine,
50 (1), 12119-12124, 2017. - Axmann Š., Mucha P.B., Pokorný M.: Steady solutions to viscous shallow water equations. The case of heavy water. Communications in Mathematical Sciences, 15 (5), 1385-1402, 2017.
- Malijevský A., Pokorný P.: Průvodce matematickými metodami, VŠCHT Praha, 2017.
- Axmann Š., Mucha P.B.: Decently regular steady solutions to the compressible NSAC system. Topological Methods in Nonlinear Analysis, 48 (1),1-27, 2016.
- Janovská D., Opfer G. : Matrices Over Nondivision Algebras Without Eigenvalues. Advances in Applied Clifford Algebras 26, 591-612, 2016.
- Bonnard B., Henninger H. C., Němcová J., Pomet J.-B.: Time Versus Energy in the Averaged Optimal Coplanar Kepler Transfer Towards Circular Orbits. Acta Applicandae Mathematicae, 135 (1), 47-80, 2015.
- Němcová J., Petreczky M., van Schuppen J.: An Algorithm for System Identification of a Discrete-Time Polynomial System without Inputs, IFAC-PapersOnLine, 48
(28), 166-171, 2015. - Axmann Š., Pokorný M.:Time-periodic solutions to the full Navier–Stokes–Fourier system with radiation on the boundary, Journal of Mathematical Analysis and Applications, 428 (1), 414-444, 2015.
- Janovská D., Opfer G.: Zeros and singular points for one-sided coquaternionic polynomials with an extension to other R4 algebras. Electronic Transaction on Numerical Analysis, 41, 133-158, 2014.
