Naše výzkumná skupina se zabývá především zkoumáním otevřených problémů v oblasti kombinatoriky, diskrétní matematiky a teorie grafů.
Oblasti výzkumu
Teorie grafů
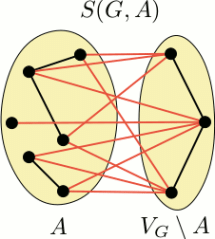
Teorie grafů nachází v posledních desetiletích mnoho aplikací v nejrůznějších oblastech lidské činnosti, od navrhování struktury sítí (elektrických, vodovodních, sociálních) přes přidělování mobilních či vysílacích frekvencí až po různé druhy optimalizace (v dopravě, ve vyhledávání atd.) Naše skupina se věnuje především studiu speciální třídy grafů odvozených od částečně uspořádaných množin, tzv. cover-incomparability graphs, jejich vlastnostem a složitosti jejich rozpoznávání. Další oblastí, která je v současné době v centru našeho zájmu je studium ekvivalencí na grafech definovaných pomocí různých grafových operací, například tzv. Seidel’s switching.
Chemická teorie grafů
V této oblasti se věnujeme především studiu tzv. Wienerova indexu molekulových grafů. Harry Wiener zavedl tento index pro určení aproximačního vzorce bodu varu parafínu.
Od té doby se Wienerův index stal jedním z nejčastěji používaných molekulových deskriptorů a v současnosti je využíván především k předběžnému screeningu molekul léčiv.
Nás zajímá především určování extremálních hodnot Wienerova indexu pro důležité třídy grafů.
Výpočetní složitost
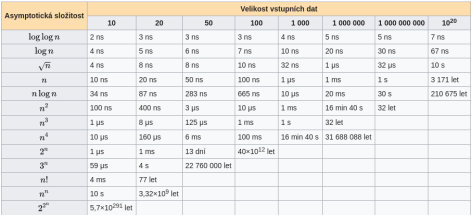
Asymptotická složitost je jedním za zásadních nástrojů, jak porovnávat efektivitu a rychlost algoritmů. Pro konkrétní problém je zajímavá hlavně jeho časová složitost vzhledem k velikosti vstupu, která může být i pro relativně jednoduché úlohy a relativně malé vstupy enormní (např. stovky let, viz uvedenou tabulku). V centru našeho zájmu je hledání hranice pro polynomiální složitost (viz známý problém P versus NP) pro různé úlohy na grafech.
Grupy reflexí a jejich aplikace
Grupy reflexí popisují mimo jiné přirozené symetrie pravidelných i částečně pravidelných n-rozměrných objektů (například Platonských těles). Studujeme vlastnosti speciálních funkcí definovaných na orbitách takovýchto grup. Příslušné symetrie využíváme například při diskrétních zobecněných fourierovských transformacích.
 Prezentační karta
Prezentační karta
Kontaktní osoby:
Y RNDr. Jana Maxová, Ph.D. - vedoucí skupiny
b jana.maxova@vscht.cz
e 22044 5039
Y Ing. Lenka Cúthová (Háková), Ph.D.
b lenka.hakova@vscht.cz
e 22044 5035
Y RNDr. Eva Jelínková, Ph.D
b eva.jelinkova@vscht.cz
e 22044 5038
Y RNDr. Pavla Pavlíková,Ph.D.
b pavla.pavlikova@vscht.cz
e 22044 5038
Y Doc. RNDr. Daniel Turzík, CSc.
b daniel.turzik@vscht.cz
e 22044 5036
Nedávné publikace
- Bok, Jan & Maxová, Jana. (2018). Characterizing Subclasses of Cover-Incomparability Graphs by Forbidden Subposets. Order. 10.1007/s11083-018-9470-7.
- Jelínek, V.; Jelínková, E.; Kratochvíl, J. On the hardness of switching to a small number of edges. Lecture Notes in Computer Science, Springer, 2016.
- Háková L.; Tereszkiewicz A. On Generalization of Special Functions Related to Weyl Groups. Acta Polytechnica, Journal of Advanced Engineering 2016, 56 (6), 440–447
- Háková L.; Hrivnák J.; Motlochová L. On cubature rules associated to weyl group orbit functions. Acta Polytechnica, Journal of Advanced Engineering 2016, 56 (3), 202–213
- Hejda, T.; Pelantová, E. Spectral properties of cubic complex Pisot units Mathematics of Computatio. 2016.
- Maxová, J.; Dubcová, M.; Pavlíková, P.; Turzík, D. Which k-trees are cover-incomparability graphs? Discrete Applied Mathematics, 2014.
- Jelínková, E.; Kratochvíl, J. On Switching to H-Free Graphs. Journal of Graph Theory, 2014.
- L.Háková, A. Tereszkiewicz, On immanant functions related to Weyl groups of A_n, J. Math. Phys., Vol.55, Issue 11, 2014
- Maxová, J.; Turzík, D. Which distance-hereditary graphs are cover-incomparability graphs? Discrete Applied Mathematics, 2013.