Studium dynamických systémů má na ÚM dlouhou tradici. První seminář, který se zabýval soustavami diferenciálních rovnic a dynamickými systémy obecně, začal pracovat už v roce 2002. V současnosti se členové ústavu zabývají širokou škálou dynamických systémů, v rovině teoretické i aplikační.
Oblasti výzkumu
Kvalitativní teorie dynamických systémů
Soustavy diferenciálních rovnic jsou vyšetřovány s důrazem na jejich geometrické a kvalitativní vlastnosti a jsou chápany jako součást obecnější kvalitativní teorie dynamických systémů.
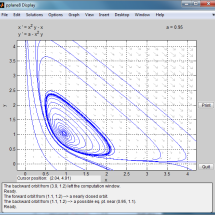
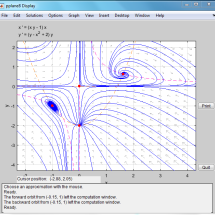
V řadě aplikací v chemickém inženýrství, biologii, teorii řízení apod. se objevuje nespojitost. Může se jednat o přirozenou součást systému nebo může být způsobena např. zásahem zvenčí.
Po částech hladké dynamické systémy mají bohatou a komplexní dynamiku. S pomocí nástrojů kvalitativní analýzy spojitých dynamických systémů můžeme zkoumat fázový portrét, stabilitu, bifurkace a další lokální i globální vlastnosti nespojitých tzv. Filippovových systémů.
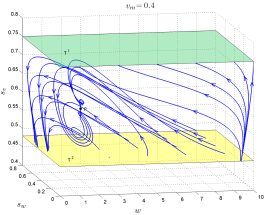
Chování systému pavouků na vinici s balónovým efektem
M. Biák: Po částech hladké dynamické systémy. Disertační práce, VŠCHT Praha, 2015
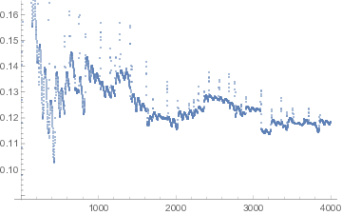
Rekonstrukce dynamiky z časových řad
Při rekonstrukci využíváme metodu časových zpoždění, která vychází z Takensovy věty o vnoření. Z časové řady, která je projekcí dynamického systému do intervalu reálné osy a tedy jen částečně popisuje dynamický systém, jsme schopni kvalitativně rekonstruovat celý dynamický systém. Metodu používáme na časové řady, které vznikají v chemických a medicinských problémech.
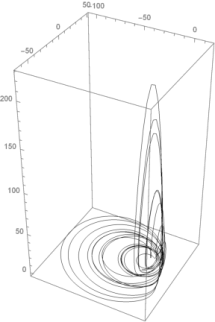
Řešení diferenciálních rovnic
Z numerických metod pro obyčejné i parciální diferenciální rovnice se zabýváme zejména metodou konečných prvků a objemů, okrajově též metodou sítí. Z analytických metod se pak zaměřujeme na využití Laplaceovy transformace pro řešení lineárních parciálních diferenciálních rovnic, které se vyskytují v technických problémech.
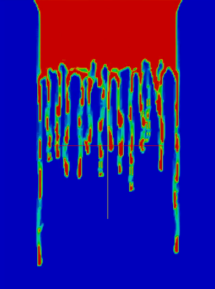
Mechanika a termodynamika tekutin
V oblasti numerického řešení úloh proudění tekutin (CFD) simulujeme s použitím softwaru OpenFOAM zejména vícefázové toky v chemicko-inženýrských aplikacích, např. v separačních kolonách. Z teoretického hlediska se pak zabýváme matematickou analýzou rovnic proudění tekutin, mimo jiné chemicky reagujících směsí.

Teorie chaosu
V teorii chaosu se zabýváme nelineárními dynamickými systémy, které vykazují složité, omezené, neutuchající, ale neperiodické chování, tzv. deterministický chaos, typický též citlivou závislostí na počátečních podmínkách.
Informační termodynamika
Informační termodynamika představuje obor spojující teorii informace s klasickou teoretickou termodynamikou. Teorie nachází aplikace v řadě fyzikálních procesů.
Teorie řízení a optimalizace
V oblasti teorie řízení studujeme modely biochemických procesů a jejich vlastnosti jako je říditelnost, pozorovatelnost či stabilita. Dále odhadujeme parametry modelu, případně provádíme simulace. Z hlediska možných aplikací nás zajímá také otázka optimalizace řízení, příp. možnost redukování dimenze modelu.
Finanční matematika
V oblasti finanční matematiky studujeme odvozené parabolické parciální rovnice pro oceňování finančních derivátů. Zajímá nás především numerické řešení speciální difuzní rovnice Blackova–Scholesova modelu pro oceňování opcí.
Numerické metody v Cliffordových algebrách
V rámci dlouhodobé spolupráce s Universitou Hamburk se zabýváme numerickou lineární algebrou pro kvaterniony a další komutativní i nekomutativní algebry v R4. V současné době hrají kvarterniony důležitou roli ve vývoji robotiky a počítačové grafiky. Coquaterniony, další z nekomutativních algeber v R4, dnes nacházejí uplatnění při modelování složitých problémů v chemii a ve fyzice, zejména kvantové.
Prezentační karta
Kontaktní osoby
Y Mgr. Šimon Axman, Ph.D. - vedoucí skupiny
b simon.axmann@vscht.cz
e 22044 5030
Y RNDr. Lenka Červená, Ph.D.
b lenka.cervena@vscht.cz
e 22044 5031
Y RNDr. Miroslava Dubcová, CSc.
b miroslava.dubcova@vscht.cz
e 22044 5031
Y Ing. Bohdan Hejna, Ph.D.
b bohdan.hejna@vscht.cz
e 22044 5037
Y Ing. Martin Isoz, Ph.D.
b martin.isoz@vscht.cz
e 22044 4349
Y Prof. RNDr. Drahoslava Janovská, CSc.
b drahoslava.janovska@vscht.cz
e 22044 5040
Y Prof. RNDr. Milan Kubíček, CSc.
b milan.kubicek@vscht.cz
e 22044 3095
Y Mgr. Jana Němcová, Ph.D.
b jana.nemcova@vscht.cz
e 22044 5038
Y Ing. Slavomír Parma, Ph.D.
b slavomir.parma@vscht.cz
e 22044 4349
Y RNDr. Pavel Pokorný, CSc.
b pavel.pokorny@vscht.cz
e 22044 5033
Y Doc. RNDr. Carmen Simerská, CSc.
b carmen.simerska@vscht.cz
e 22044 5040
Nedávné publikace
- Janovska, Drahoslava; Opfer, Gerhard: The Relation Between the Companion Matrix and the Companion Polynomial in R-4 Algebras, ADVANCES IN APPLIED CLIFFORD ALGEBRAS, Volume: 28, Issue: 4, Article Number: UNSP 76, Published: SEP 2018
- Isoz M., Haidl J.: CFD analysis of gas flow through corrugated sheet structured packing: Effects of packing geometry. Industrial & Engineering Chemistry Research, 57(34), 11785–11796, 2018.
- van Schuppen J., Xi K., Němcová J.: A Subalgebraic Procedure for System Identification of a Continuous-Time Polynomial System. IFAC-PapersOnLine, 51, 395-400, 2018.
- Hejna B.: Information Transfer and Thermodynamic Point of View on Goedel Proof, in Ontology in Information Science, 280-300, 2018.
- Axmann Š., Mucha P.B., Pokorný M.: Steady solutions to the Navier-Stokes-Fourier system for dense compressible fluid. Topol. Methods Nonlinear Anal., 52, 2018.
- Hejna B.: Informační termodynamika IV. ; Goedelovy věty, přenos informace, termodynamika a Caratheodoryho věty, VŠCHT Praha, 2017.
- Kočí P., Isoz M. et.al. 3D reconstruction and pore-scale modeling of coated catalytic filters for automotive exhaust gas aftertreatment. Catalysis Today, 2017.
- Janovská D., Opfer G.: The number of zeros of unilateral polynomials over coquaternions and related algebras. Electronic Transaction on Numerical Analysis, 46, 55-70, 2017.
- Němcová J., van Schuppen J.: Checking Algebraic Reachability of Polynomial and Rational Systems, IFAC-PapersOnLine,
50 (1), 12119-12124, 2017. - Axmann Š., Mucha P.B., Pokorný M.: Steady solutions to viscous shallow water equations. The case of heavy water. Communications in Mathematical Sciences, 15 (5), 1385-1402, 2017.
- Malijevský A., Pokorný P.: Průvodce matematickými metodami, VŠCHT Praha, 2017.
- Axmann Š., Mucha P.B.: Decently regular steady solutions to the compressible NSAC system. Topological Methods in Nonlinear Analysis, 48 (1),1-27, 2016.
- Janovská D., Opfer G. : Matrices Over Nondivision Algebras Without Eigenvalues. Advances in Applied Clifford Algebras 26, 591-612, 2016.
- Bonnard B., Henninger H. C., Němcová J., Pomet J.-B.: Time Versus Energy in the Averaged Optimal Coplanar Kepler Transfer Towards Circular Orbits. Acta Applicandae Mathematicae, 135 (1), 47-80, 2015.
- Němcová J., Petreczky M., van Schuppen J.: An Algorithm for System Identification of a Discrete-Time Polynomial System without Inputs, IFAC-PapersOnLine, 48
(28), 166-171, 2015. - Axmann Š., Pokorný M.:Time-periodic solutions to the full Navier–Stokes–Fourier system with radiation on the boundary, Journal of Mathematical Analysis and Applications, 428 (1), 414-444, 2015.
- Janovská D., Opfer G.: Zeros and singular points for one-sided coquaternionic polynomials with an extension to other R4 algebras. Electronic Transaction on Numerical Analysis, 41, 133-158, 2014.
