| 1. |
Lineární algebra |
připomenutí základů lineární algebry z MI a MII,
Gauss-Jordanova eliminace, lineární algebra v prostředí Matlab |
   |
| 2. |
Chemické sítě |
tvorba stechiometrické matice
hledání reakčních cest |
 |
| 3. |
Singulární rozklad matice |
vlastní čísla a vlastní vektory matic
charakteristický polynom, spektrum matice
singulární rozklad matice |
 |
|
| 4. |
Lineární a nelineární regrese |
metoda nejmenších čtverců
linearizace
řešení normálních rovnic |
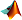 |
|
| 5. |
Implicitně definované funkce |
derivace implicitně definovaných funkcí
tečné přímky a roviny |
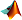 |
| 6. |
Soustavy obyčejných diferenciálních rovnic |
připomenutí teorie ODR
analytické řešení ODR
obecné a partikulární řešení |
|
|
| 7. |
Soustavy obyčejných diferenciálních rovnic
numerické řešení, počáteční úloha |
numerické řešení SODR
Eulerova metoda, metody Runge-Kutta |
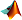 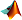 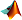   |
| 8. |
Soustavy obyčejných diferenciálních rovnic
numerické řešení, okrajová úloha |
numerické řešení SODR
metoda střelby
Newtonova metoda |
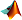 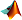 |
| 9. |
Soustavy lineárních diferenciálních rovnic |
analytické řešení LSODR |
 |
| 10. |
Fázové portréty lineárních soustav |
vyšetření fázových portrétů lineárních soustav
sedlo, uzel, centr, ohnisko |
|
| 11. |
Fázové portréty nelineárních soustav |
linearizace okolí stacionárních stavů
klasifikace stacionárních stavů
sedlo, uzel, ohnisko
homoklinické a heteroklinické trajektorie
uzavřené trajektorie soustavy |
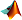  |
| 12. |
Úvod do vektorové analýzy |
operátor Nabla
divergence a rotace vektorového pole
Greenova věta, Gaussova věta |
|
| 13. |
Křivkový a plošný integrál |
křivkový integrál skalárního a vektorového pole
plošný integrál skalárního a vektorového pole |
 |
| 14. |
Fourierovy řady |
aproximace funkcí Fourierovými řadami
řešení 1-D rovnice vedení tepla |
 |